nanaxev.blogg.se

• #Delaunay Triangulation 2D Code That Does

Delaunay Triangulation 2D Code That Does

From scipy.spatial import DelaunayConstrained and Delaunay constrained triangulations. I also made it self-contained so it doesn't depend on an outside library. I modified the alpha-shape (concave hull) computation from here so that it doesn't insert inner edges (the only_outer parameter). A Delaunay triangulation fulfills the following empty circle property (also called Delaunay property ): the circumscribing circle of any facet of the triangulation contains no data point in its interior.Here is some Python code that does what you need. The class Delaunaytriangulation2 is designed to represent the Delaunay triangulation of a set of data points in the plane.

But I'm having trouble reproducing the same results that I have with delaunay(). I know that I need to use delaunayTriangulation(). However, the delaunay function will not allow me to access the vertices of the triangles so that I can perform the 'etching' reaction.

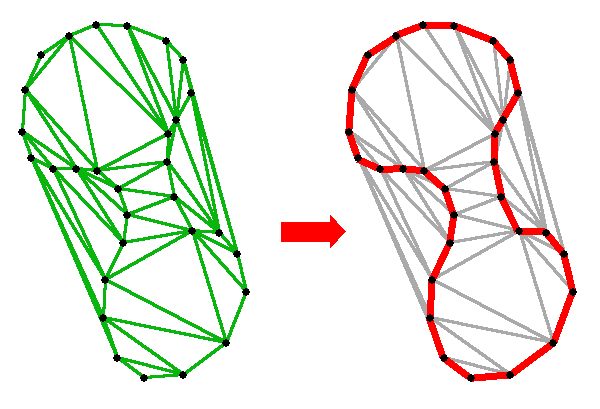
From matplotlib.tri import TriangulationIdxs = np.vstack(list(np.where(mpl_tri.neighbors = -1))).TUnique_edges.append((mpl_tri.triangles,If unique_edges != unique_edges:Unique_edges = unique_edges)Unique_edges] = unique_edges]Ring_collection.append(unique_edges)# if there is just one ring, the exception is never reached,# so populate ring_collection before returning.Ring_collection.append(np. The reasoning is that# boundary edges appear only once while interior edges twiceEdges = Count = Counter(edges) # count occurrences of each edge# keep only edges that appear one time (concave hull edges)# these are the coordinates of the edges that comprise the concave hullEdges = ], points]) for e in edges ]# use this only if you need to return your hull points in "order" (i think its CCW)Hull_vertices = boundary.exterior.coords.xyBuilding up on answer, I used the following algorithm to calculate the boundary rings of a Delaunay triangulation. / alpha # Radius Filter based on alpha value# now a main difference with the aforementioned approaches is that we dont use a Set()# because this eliminates duplicate edges.# in the list below both (i, j) and (j, i) pairs are counted.